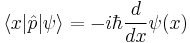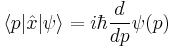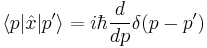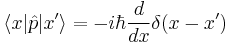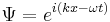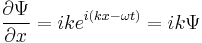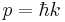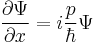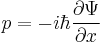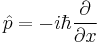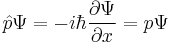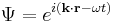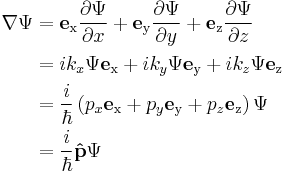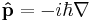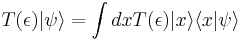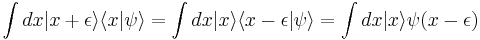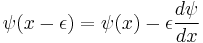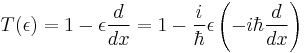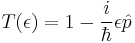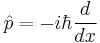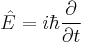Momentum operator
In quantum mechanics, momentum is defined as an operator on the wave function. The Heisenberg uncertainty principle defines limits on how accurately the momentum and position of a single observable system can be known at once. In quantum mechanics, position and momentum are conjugate variables.
Contents[hide] |
Definition
For a single particle with no electric charge and no spin, the momentum operator can be written in the position basis as: [1]
where ∇ is the gradient operator, ħ is the reduced Planck constant, and i is the imaginary unit.
In one spatial dimension this becomes:
This is a commonly encountered form of the momentum operator, though not the most general one. For a charged particle q in an electromagnetic field, described by the scalar potential φ and vector potential A, the momentum operator must be replaced by the kinetic momentum operator, which includes a contribution from the A field: [2]
where 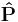 is the canonical momentum operator given as the usual momentum operator:
is the canonical momentum operator given as the usual momentum operator:
so the momentum operator generalizes to
This is of course true for electrically charged or neutral particles, since the second term vanishes if q is zero and the original operator appears.
Properties
Hermiticity
The momentum operator is always a Hermitian operator when it acts on physical (in particular, normalizable) quantum states.[3]
Canonical commutation relation
One can easily show that by appropriately using the momentum basis and the position basis:
Fourier transform
One can show that the Fourier transform of the momentum in quantum mechanics is the position operator. The Fourier transform turns the momentum-basis into the position-basis.
The same applies for the Position operator in the momentum basis:
and other useful relations:
where 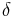 stands for Dirac's delta function.
stands for Dirac's delta function.
Derivations
De Broglie plane waves
The momentum and energy operators can easily be constructed in the following way. [4] Starting in one dimension, using the plane wave solution to Schrödinger's equation:
The first order partial derivative with respect to space is
by the De Broglie relation:
we have
The momentum value p is a scalar factor, the momentum of the particle and the value that is mesured. Cancellation of Ψ leads to
The partial derivative is a linear operator so this expression can only be the momentum operator:
So it can be concluded that the scalar p is the eigenvalue of the operator, while 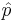 is the operator. Summarizing these results:
is the operator. Summarizing these results:
The derivation in three dimensions is the same, except using the gradient operator instead of one partial derivative. In three dimensions, the plane wave solution to Schrödinger's equation is:
The gradeint is
hence
Since the operators are linear, they are valid for any linear combination of plane waves, and so they can act on any wavefunction without affecting the properties of the wavefunction or operators.
Infinitesimal translations
Suppose we have an infinitesimal translation operator 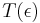 , where
, where  represents the length of the infinitesimal translation, then
represents the length of the infinitesimal translation, then
that becomes
We assume the function  to be analytic (or simply differentiable, for simplicity), so we may write:
to be analytic (or simply differentiable, for simplicity), so we may write:
so we have for infinitesimal values of epsilon:
we know from classical mechanics that momentum is the generator of translation, so we know that
thus
See also
References
- ^ Quantum Mechanics Demystified, D. McMahon, Mc Graw Hill (USA), 2006, ISBN(10) 0 07 145546 9
- ^ Quantum Physics of Atoms, Molecules, Solids, Nuclei and Particles (2nd Edition), R. Resnick, R. Eisberg, John Wiley & Sons, 1985, ISBN 978-0-471-873730
- ^ See Lecture notes 1 by Robert Littlejohn for a specific mathematical discussion and proof for the case of a single, uncharged, spin-zero particle. See Lecture notes 4 by Robert Littlejohn for the general case.
- ^ Quantum Physics of Atoms, Molecules, Solids, Nuclei and Particles (2nd Edition), R. Resnick, R. Eisberg, John Wiley & Sons, 1985, ISBN 978-0-471-873730
|
||||||||
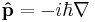
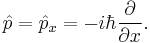
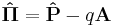
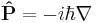
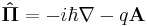
![\left [ \hat{ x }, \hat{ p } \right ] = \hat{x} \hat{p} - \hat{p} \hat{x} = i \hbar.](/2012-wikipedia_en_all_nopic_01_2012/I/00f5aa11f9413f325fb0b7f4fe3efe2d.png)